|
BIFL Data
Analyzer (BIFLDA) is intended for sliding analysis of fluorescence decays and correlation
functions built from BIFL data (B&H SPC, PicoQuant TimeHarp 200, PicoHarp
300 and Symphotime-64bit) using Maximum Likelihood (ML) method. Inter arrival time distribution (IATD)
coincidence analysis is also supported.
Data Management
more...
Import of B&H SPC data: SPC-402/432, SPC-401/431, SPC-6x0/256ch,
SPC-6x0/4096ch, SPC-830 and other complementary to SPC-830 data formats (SPC-130/134, SPC-140/144, SPC-150/154) (up to four channels)
-
Import of PicoQuant TimeHarp 200, PicoHarp 300 and Symphotime-64bit (up to four channels)
-
Calculation of absolute photon arrival times when possible
Macro & micro
time processing
Automatic and manual
Burst selection in the intensity and time lag plot
Sliding by either
selected bursts or constant time or constant amount of photons
Calculation of
fluorescence decays and anisotropy
Calculation of autocorrelation functions (with and without the normalization)
and inter arrival time distribution in linear and quasi-logarithmic time scales
Binning of fluorescence decays
Calculation and
plotting Energy Transfer Efficiency and Fractional Intensity for two
color data
Calculation and
plotting Steady State Polarization and Anisotropy for polarized data
Selecting
user-defined time regions, start and end analysis channels with
cursors
Displaying
fluorescence and triplet lifetimes histogram
Export data to ASCII
file
-
Export autocorrelation functions to
ConfoCor formatted
file
Analysis Methods
more...
Sliding
analysis (Maximum Likelihood with multinomial statistics and
Levenberg-Marquardt optimization algorithm)
Analysis
of selected dataset
Automatic
shift detection
Fit
with and without convolution
Correction
for the background
Automatically
generated initial guesses
Parameter
fixing and constraints
Confidence
intervals by standard errors
Quality
of fit: MLE criterion value and visual inspection of residuals and
autocorrelation of residuals
FCS
analysis
-
IATD coincidence
analysis
Analysis
Models
more...
Fluorescence
decay analysis
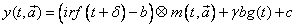
where:
– d
is time shift;
– b
is level of dark noise;
– g
is background multiplication factor;
– с
time-uncorrelated background;|
– irf(t)
is measured instrument response function;
– bg(t)
is measured background (optional);
Anisotropy
analysis
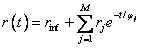
where:
–
rinf is anisotropy when t → ∞;
– rj
are pre-exponential factors;
– jj
are rotational correlation times;
– M
is number of exponents.
Analysis
of autocorrelation function for immobilized molecules

where:
–
cj are pre-exponential factors;
– tj
are triplet-state lifetimes;
– K
is number of exponents.
Analysis
of autocorrelation function for molecules in solution (FCS)

where:
–
F and t are
triplet-state fraction and lifetime;
– N
is an average number of molecules in observation volume;
– Fj
are fractions of corresponding diffusion components;
– TDj
are diffusion times of corresponding diffusion components;
Model library is easily extendable
| 
